quarta-feira, 15 de junho de 2016
Entrega de trabalhos na forma digital
Caros alunos, os trabalhos que eu mencionar que podem ser entregues na forma digital podem ser enviados para o email
Atenção, pois somente alguns trabalhos poderão ser entregues na forma digital. Será avisado quando isso puder ser feito.
domingo, 12 de junho de 2016
A natureza do calor
Adaptado do livro Física Básica de H. Moysés Nussensveig
No final do século 18 existiam duas hipóteses alternativas sobre a natureza do calor. A hipótese mais aceita considerava o calor como uma substância fluida indestrutível que “preencheria os poros” dos corpos e se escoaria de um corpo mais quente a um mais frio. Lavoisier chamou essa substância hipotética de “calórico”. A implicação era que o calor pode ser transferido de um corpo a outro, mas a quantidade total de “calórico” se conservaria, ou seja, existiria uma lei de conservação do calor.
A hipótese rival, endossada entre outros por Francis Bacon e Robert Hooke, foi assim expressa por Newton em 1704: “O calor consiste num minúsculo movimento de vibração das partículas dos corpos”. Ideias deste gênero podem ter sido sugeridas pela geração de calor por atrito, exemplificada pelo “método dos escoteiros” para acender uma fogueira, ou pelo aquecimento do ferro martelado numa bigorna. A teoria do calórico explicava estes efeitos dizendo que o atrito, ou o martelo do ferreiro, “espremem” o calórico para fora do material, como água absorvida numa esponja.
Um dos primeiros a apontar dificuldades com a teoria do calórico foi Benjamin Thomson, um aventureiro que se tornou Conde de Rumford na Bavária (e casou-se com a viúva de Lavoisier). Uma das dificuldades era que experiências bastante precisas, feitas por Rumford, não detectavam qualquer variação do peso de um corpo acompanhando a absorção ou eliminação de grandes quantidades de calor. Entretanto, o calórico poderia ser um fluido imponderável, a exemplo do que se acreditava valer para a eletricidade.
A principal dificuldade, porém, estava na “lei de conservação do calórico”, pois a quantidade de calórico que podia ser ‘espremida para fora” de um corpo por atrito era ilimitada. Com efeito, em 1798, Rumford escreveu:
“Foi por acaso que me vi levado a realizar as experiências que vou relatar agora... Estando ocupado, ultimamente, em supervisionar a perfuração de canhões nas oficinas do arsenal militar de Munich, chamou-me a atenção o elevado grau de aquecimento de um canhão de bronze, atingido em tempos muito curtos, durante o processo de perfuração; bem como a temperatura ainda mais alta (acima do ponto de ebulição da água, conforme verifiquei) das aparas metálicas removidas pela perfuração.
Meditando sobre os resultados dessas experiências, somos naturalmente levados à grande questão que tem sido objeto de tantas especulações filosóficas, ou seja:
Que é o calor? Existe um fluido ígneo? Existe alguma coisa que possamos chamar de calórico?
Vimos que uma quantidade muito grande de calor pode ser produzida pelo atrito de duas superfícies metálicas, e emitida num fluxo constante em todas as direções, sem interrupção, e sem qualquer sinal de diminuição ou exaustão...
... A fonte de calor gerado por atrito nessas experiências parece ser inesgotável. É desnecessário acrescentar que algo que qualquer corpo ou sistema de corpos isolado pode continuar fornecendo sem limites, não pode ser uma substância material, e me parece extremamente difícil, senão impossível, conceber qualquer coisa capaz de ser produzida ou transmitida da forma como o calor o era nessas experiências, exceto o MOVIMENTO”.
Rumford foi assim levado a endossar a teoria alternativa de que “... o calor não passa de um movimento vibratório que tem lugar entre as partículas do corpo”.
A máquina a vapor de James Watt, desenvolvida na segunda metade do século 18, era uma demonstração prática de que o calor leva à capacidade de produzir trabalho. Entretanto, a conexão entre calor e energia só foi estabelecida no século 19.
Um dos primeiros a discutir essa conexão foi o médico alemão Julius Robert Mayer. Aparentemente, ele foi levado, a refletir sobre o problema quando, como médico de bordo durante uma viagem aos trópicos, observou que o sangue venoso parecia ser mais vermelho que nos climas frios da Europa, o que o conduziu a especulações sobre a origem do calor animal. Assim, em 1842, Mayer chegou ao primeiro enunciado geral do Princípio de Conservação da Energia:
“As energias são entidades conversíveis, mas indestrutíveis... Em inúmeros casos, vemos que um movimento cessa sem ter produzido quer outro movimento” (energia cinética) “quer o levantamento de um peso” (energia potencial), “mas a energia, uma vez que existe, não pode ser aniquilada; pode somente mudar de forma, e daí surge a questão: Que outras formas pode ela assumir? Somente a experiência pode levar-nos a uma conclusão”.
A experiência mostra que o trabalho pode (por exemplo através do atrito) ser convertido em calor. Logo, diz Mayer, “Se energia cinética e potencial são equivalentes a calor, é natural que calor seja equivalente à energia cinética e potencial”. Ou seja, o calor é uma forma de energia.
Mayer enunciou então um problema crucial: “Quão grande é a quantidade de calor que corresponde a uma dada quantidade de energia cinética ou potencial? “Ou seja, qual é a “taxa de conversão” entre energia mecânica (medida em Joules) e calor (medido em “calorias”)? Este é o problema da determinação do equivalente mecânico da caloria.
Com extraordinária sagacidade, Mayer conseguiu inferir a resposta partindo de um dado experimental já conhecido na época: a diferença entre o calor específico de um gás a pressão constante e seu calor específico a volume constante. Usando os resultados então conhecidos (cuja incerteza experimental era grande), Mayer deduziu um valor do equivalente mecânico da caloria cuja diferença do valor correto é da ordem de 10%. Entretanto, seu trabalho foi considerado muito especulativo e foi ignorado durante as duas décadas seguintes.
As experiências básicas para a obtenção do equivalente mecânico da caloria foram realizadas durante um período de quase 30 anos pelo cervejeiro e cientista amador inglês James Prescott Joule. Seus primeiros resultados, anunciados em 1843, eram ainda muito imprecisos, mas em 1868 ele chegou finalmente a resultados de grande precisão.
Quando Joule apresentou um dos primeiros resultados confiáveis, numa reunião realizada em Oxford em 1847, só despertou o interesse de um jovem da audiência: William Thomson, o futuro Lord Kelvin. Três dias depois, Joule se casou. Duas semanas mais tarde, Thomson, em Chamonix, encontrou Joule, munido de um imenso termômetro, subindo ao topo de uma cachoeira. Mesmo em lua de mel, queria verificar a diferença de temperatura que deveria existir, conforme seus cálculos, entre a água em cima e em baixo da cachoeira (para as cataratas de Niagara, ele estimou essa diferença em ~0,2°C)!
A formulação mais geral do Princípio de Conservação da Energia foi apresentada pelo físico matemático-fisiologista Hermann von Helmholtz numa reunião da Sociedade Física de Berlim, em 23 de julho de 1847. Helmholtz mostrou que ele se aplicava a todos os fenômenos então conhecidos - mecânicos, térmicos, elétricos, magnéticos; também na físico-química, na astronomia e na biologia (metabolismo dos seres vivos).
Em seu livro “Sobre a Conservação da Energia” (Helmholtz ainda usava a palavra “força” em lugar de “energia”; a energia cinética era chamada de “força viva”), ele diz:
... “chegamos à conclusão de que a natureza como um todo possui um estoque de energia que não pode de forma alguma ser aumentado ou reduzido; e que, por conseguinte, a quantidade de energia na natureza é tão eterna e inalterável como a quantidade de matéria. Expressa desta forma, chamei esta lei geral de “Princípio de Conservação da Energia”.
Por volta de 1860, o Princípio de Conservação da Energia, que corresponde, conforme veremos, à 1ª lei da termodinâmica, já havia sido reconhecido como um princípio fundamental, aplicável a todos os fenômenos conhecidos.
Versão para impressão
No final do século 18 existiam duas hipóteses alternativas sobre a natureza do calor. A hipótese mais aceita considerava o calor como uma substância fluida indestrutível que “preencheria os poros” dos corpos e se escoaria de um corpo mais quente a um mais frio. Lavoisier chamou essa substância hipotética de “calórico”. A implicação era que o calor pode ser transferido de um corpo a outro, mas a quantidade total de “calórico” se conservaria, ou seja, existiria uma lei de conservação do calor.
A hipótese rival, endossada entre outros por Francis Bacon e Robert Hooke, foi assim expressa por Newton em 1704: “O calor consiste num minúsculo movimento de vibração das partículas dos corpos”. Ideias deste gênero podem ter sido sugeridas pela geração de calor por atrito, exemplificada pelo “método dos escoteiros” para acender uma fogueira, ou pelo aquecimento do ferro martelado numa bigorna. A teoria do calórico explicava estes efeitos dizendo que o atrito, ou o martelo do ferreiro, “espremem” o calórico para fora do material, como água absorvida numa esponja.
Um dos primeiros a apontar dificuldades com a teoria do calórico foi Benjamin Thomson, um aventureiro que se tornou Conde de Rumford na Bavária (e casou-se com a viúva de Lavoisier). Uma das dificuldades era que experiências bastante precisas, feitas por Rumford, não detectavam qualquer variação do peso de um corpo acompanhando a absorção ou eliminação de grandes quantidades de calor. Entretanto, o calórico poderia ser um fluido imponderável, a exemplo do que se acreditava valer para a eletricidade.
A principal dificuldade, porém, estava na “lei de conservação do calórico”, pois a quantidade de calórico que podia ser ‘espremida para fora” de um corpo por atrito era ilimitada. Com efeito, em 1798, Rumford escreveu:
“Foi por acaso que me vi levado a realizar as experiências que vou relatar agora... Estando ocupado, ultimamente, em supervisionar a perfuração de canhões nas oficinas do arsenal militar de Munich, chamou-me a atenção o elevado grau de aquecimento de um canhão de bronze, atingido em tempos muito curtos, durante o processo de perfuração; bem como a temperatura ainda mais alta (acima do ponto de ebulição da água, conforme verifiquei) das aparas metálicas removidas pela perfuração.
Meditando sobre os resultados dessas experiências, somos naturalmente levados à grande questão que tem sido objeto de tantas especulações filosóficas, ou seja:
Que é o calor? Existe um fluido ígneo? Existe alguma coisa que possamos chamar de calórico?
Vimos que uma quantidade muito grande de calor pode ser produzida pelo atrito de duas superfícies metálicas, e emitida num fluxo constante em todas as direções, sem interrupção, e sem qualquer sinal de diminuição ou exaustão...
... A fonte de calor gerado por atrito nessas experiências parece ser inesgotável. É desnecessário acrescentar que algo que qualquer corpo ou sistema de corpos isolado pode continuar fornecendo sem limites, não pode ser uma substância material, e me parece extremamente difícil, senão impossível, conceber qualquer coisa capaz de ser produzida ou transmitida da forma como o calor o era nessas experiências, exceto o MOVIMENTO”.
Rumford foi assim levado a endossar a teoria alternativa de que “... o calor não passa de um movimento vibratório que tem lugar entre as partículas do corpo”.
A máquina a vapor de James Watt, desenvolvida na segunda metade do século 18, era uma demonstração prática de que o calor leva à capacidade de produzir trabalho. Entretanto, a conexão entre calor e energia só foi estabelecida no século 19.
Um dos primeiros a discutir essa conexão foi o médico alemão Julius Robert Mayer. Aparentemente, ele foi levado, a refletir sobre o problema quando, como médico de bordo durante uma viagem aos trópicos, observou que o sangue venoso parecia ser mais vermelho que nos climas frios da Europa, o que o conduziu a especulações sobre a origem do calor animal. Assim, em 1842, Mayer chegou ao primeiro enunciado geral do Princípio de Conservação da Energia:
“As energias são entidades conversíveis, mas indestrutíveis... Em inúmeros casos, vemos que um movimento cessa sem ter produzido quer outro movimento” (energia cinética) “quer o levantamento de um peso” (energia potencial), “mas a energia, uma vez que existe, não pode ser aniquilada; pode somente mudar de forma, e daí surge a questão: Que outras formas pode ela assumir? Somente a experiência pode levar-nos a uma conclusão”.
A experiência mostra que o trabalho pode (por exemplo através do atrito) ser convertido em calor. Logo, diz Mayer, “Se energia cinética e potencial são equivalentes a calor, é natural que calor seja equivalente à energia cinética e potencial”. Ou seja, o calor é uma forma de energia.
Mayer enunciou então um problema crucial: “Quão grande é a quantidade de calor que corresponde a uma dada quantidade de energia cinética ou potencial? “Ou seja, qual é a “taxa de conversão” entre energia mecânica (medida em Joules) e calor (medido em “calorias”)? Este é o problema da determinação do equivalente mecânico da caloria.
Com extraordinária sagacidade, Mayer conseguiu inferir a resposta partindo de um dado experimental já conhecido na época: a diferença entre o calor específico de um gás a pressão constante e seu calor específico a volume constante. Usando os resultados então conhecidos (cuja incerteza experimental era grande), Mayer deduziu um valor do equivalente mecânico da caloria cuja diferença do valor correto é da ordem de 10%. Entretanto, seu trabalho foi considerado muito especulativo e foi ignorado durante as duas décadas seguintes.
As experiências básicas para a obtenção do equivalente mecânico da caloria foram realizadas durante um período de quase 30 anos pelo cervejeiro e cientista amador inglês James Prescott Joule. Seus primeiros resultados, anunciados em 1843, eram ainda muito imprecisos, mas em 1868 ele chegou finalmente a resultados de grande precisão.
Quando Joule apresentou um dos primeiros resultados confiáveis, numa reunião realizada em Oxford em 1847, só despertou o interesse de um jovem da audiência: William Thomson, o futuro Lord Kelvin. Três dias depois, Joule se casou. Duas semanas mais tarde, Thomson, em Chamonix, encontrou Joule, munido de um imenso termômetro, subindo ao topo de uma cachoeira. Mesmo em lua de mel, queria verificar a diferença de temperatura que deveria existir, conforme seus cálculos, entre a água em cima e em baixo da cachoeira (para as cataratas de Niagara, ele estimou essa diferença em ~0,2°C)!
A formulação mais geral do Princípio de Conservação da Energia foi apresentada pelo físico matemático-fisiologista Hermann von Helmholtz numa reunião da Sociedade Física de Berlim, em 23 de julho de 1847. Helmholtz mostrou que ele se aplicava a todos os fenômenos então conhecidos - mecânicos, térmicos, elétricos, magnéticos; também na físico-química, na astronomia e na biologia (metabolismo dos seres vivos).
Em seu livro “Sobre a Conservação da Energia” (Helmholtz ainda usava a palavra “força” em lugar de “energia”; a energia cinética era chamada de “força viva”), ele diz:
... “chegamos à conclusão de que a natureza como um todo possui um estoque de energia que não pode de forma alguma ser aumentado ou reduzido; e que, por conseguinte, a quantidade de energia na natureza é tão eterna e inalterável como a quantidade de matéria. Expressa desta forma, chamei esta lei geral de “Princípio de Conservação da Energia”.
Por volta de 1860, o Princípio de Conservação da Energia, que corresponde, conforme veremos, à 1ª lei da termodinâmica, já havia sido reconhecido como um princípio fundamental, aplicável a todos os fenômenos conhecidos.
Versão para impressão
quinta-feira, 3 de março de 2016
Alessandro Volta (1745-1827): Invenção da Pilha Elétrica
Alessandro Volta (1745-1827) foi o cientista italiano responsável pela invenção de um dispositivo que revolucionou o estudo do eletromagnetismo: a bateria elétrica, ou melhor dizendo, a pilha.
A pilha de Volta foi o dispositivo que viabilizou o estudo do eletromagnetismo. Antes só haviam meios de gerar eletricidade estática através de mecanismos por fricção, como o gerador de Otto von Guericke (1602-1686), consequentemente gerando pouca corrente elétrica. A única forma conhecida de armazenar a energia eletrostática eram as garrafas de Leiden, que mesmo assim só armazenavam o suficiente para fornecer a carga acumulada por alguns instantes. A pilha de Volta foi o primeiro dispositivo estático que era capaz de gerar corrente elétrica suficiente e de maneira contínua para que fosse possível estudar os efeitos dinâmicos da eletricidade.
Ele empilhou alternadamente discos de zinco e de cobre, separando-os por pedaços de tecido embebidos em solução de ácido sulfúrico. A pilha de Volta produzia energia elétrica quando um fio condutor era ligado aos discos de zinco e de cobre, colocados na extremidade da pilha.
Sua invenção foi divulgada à comunidade científica através de um carta enviada a Royal Society em Londres no ano de 1800. Nesta carta, intitulada "Sobre a eletricidade excitada pelo simples contato entre substâncias condutoras de tipos diferentes", ele descreve a sua invenção. Volta descobriu o efeito onde dois metais diferentes, quando postos em um líquido condutor, são fonte de energia elétrica.
Na linguagem moderna dizemos que a bateria é um dispositivo que transforma energia química em energia elétrica através de oxirredução. É uma fonte de energia para circuitos elétricos.
Volta descreveu arranjos diversos para associar as baterias em série de forma a aumentar seus efeitos e sugeriu inúmeras experiências para verificar a natureza elétrica dos efeitos produzidos por seu invento comparando-o à garrafa de Leiden. Ele também propõe experimentos para demonstrar que, diferente das garrafas de Leiden, o seu invento era uma fonte de energia elétrica inesgotável, não necessitando ser carregado por outros dispositivos geradores de eletricidade como era feito com as garrafas de Leiden.
A invenção da pilha voltaica foi motivada por uma discórdia profissional sobre a resposta galvânica, segundo a qual os metais produziriam eletricidade apenas em contato com tecido animal, proposta por Luigi Galvani (1737-1798). Volta criou a primeira pilha utilizando material inorgânico entre os dois metais diferentes.
Alessandro Volta propôs experimentos para examinar os efeitos da eletricidade nos órgãos sensoriais. Ele fez algo que não é recomendado (NÃO FAÇAM ISSO EM CASA!!!): foi cobaia de seus próprios experimentos. Volta testou a sensação de conectar os fios da bateria em seus olhos e seus ouvidos.
Ainda na mesma carta enviada à Royal Society, ele examina similaridades no órgão gerador de eletricidade em peixes elétricos com a sua invenção. Ele argumenta que o sua invenção tem semelhança estrutural com o órgão produtor de eletricidade nos peixes elétricos, que parecem ser da forma de discos empilhados. Conclui que o mesmo fenômeno deve estar envolvido na sua invenção e na produção de eletricidade pelos peixes elétricos.
Volta determinou que os melhores pares de metais dissimilares para a produção de eletricidade eram o zinco e a prata.
Inicialmente, Volta experimentou células individuais em série. Cada célula era formada por um cálice de vinho cheio de salmoura na qual dois eletrodos diferentes eram mergulhados. Na pilha elétrica ele fez os eletrodos na forma de discos e substituiu o cálice por cartões embebidos em salmoura, fazendo a ligação em série das células simplesmente empilhando uma célula sobre outra.
Desta maneira a tensão máxima que a pilha poderia produzir era limitada pelo número máximo de células em série, pois a pressão exercida pelas células de cima espremiam toda a salmoura do cartão da célula de baixo.
Nas duas primeiras décadas do séc. XIX, após a invenção da pilha, houve evolução acelerada na área da eletroquímica.
A seguir temos a proposta de um experimento para fazer uma pilha com moedas e papel alumínio.
Mais abaixo, nas referências, há o endereço para uma tradução da carta original de Alessandro Volta à Royal Society, comunicando a invenção da pilha voltaica.
 |
| Alessandro Volta (1745-1827) Fonte: Wikipédia, a enciclopédia livre |
Ele empilhou alternadamente discos de zinco e de cobre, separando-os por pedaços de tecido embebidos em solução de ácido sulfúrico. A pilha de Volta produzia energia elétrica quando um fio condutor era ligado aos discos de zinco e de cobre, colocados na extremidade da pilha.
 |
| Pilha de Volta (1800) Fonte: Wikipédia, a enciclopédia livre |
Sua invenção foi divulgada à comunidade científica através de um carta enviada a Royal Society em Londres no ano de 1800. Nesta carta, intitulada "Sobre a eletricidade excitada pelo simples contato entre substâncias condutoras de tipos diferentes", ele descreve a sua invenção. Volta descobriu o efeito onde dois metais diferentes, quando postos em um líquido condutor, são fonte de energia elétrica.
Na linguagem moderna dizemos que a bateria é um dispositivo que transforma energia química em energia elétrica através de oxirredução. É uma fonte de energia para circuitos elétricos.
Volta descreveu arranjos diversos para associar as baterias em série de forma a aumentar seus efeitos e sugeriu inúmeras experiências para verificar a natureza elétrica dos efeitos produzidos por seu invento comparando-o à garrafa de Leiden. Ele também propõe experimentos para demonstrar que, diferente das garrafas de Leiden, o seu invento era uma fonte de energia elétrica inesgotável, não necessitando ser carregado por outros dispositivos geradores de eletricidade como era feito com as garrafas de Leiden.
A invenção da pilha voltaica foi motivada por uma discórdia profissional sobre a resposta galvânica, segundo a qual os metais produziriam eletricidade apenas em contato com tecido animal, proposta por Luigi Galvani (1737-1798). Volta criou a primeira pilha utilizando material inorgânico entre os dois metais diferentes.
Alessandro Volta propôs experimentos para examinar os efeitos da eletricidade nos órgãos sensoriais. Ele fez algo que não é recomendado (NÃO FAÇAM ISSO EM CASA!!!): foi cobaia de seus próprios experimentos. Volta testou a sensação de conectar os fios da bateria em seus olhos e seus ouvidos.
Ainda na mesma carta enviada à Royal Society, ele examina similaridades no órgão gerador de eletricidade em peixes elétricos com a sua invenção. Ele argumenta que o sua invenção tem semelhança estrutural com o órgão produtor de eletricidade nos peixes elétricos, que parecem ser da forma de discos empilhados. Conclui que o mesmo fenômeno deve estar envolvido na sua invenção e na produção de eletricidade pelos peixes elétricos.
Volta determinou que os melhores pares de metais dissimilares para a produção de eletricidade eram o zinco e a prata.
Inicialmente, Volta experimentou células individuais em série. Cada célula era formada por um cálice de vinho cheio de salmoura na qual dois eletrodos diferentes eram mergulhados. Na pilha elétrica ele fez os eletrodos na forma de discos e substituiu o cálice por cartões embebidos em salmoura, fazendo a ligação em série das células simplesmente empilhando uma célula sobre outra.
Desta maneira a tensão máxima que a pilha poderia produzir era limitada pelo número máximo de células em série, pois a pressão exercida pelas células de cima espremiam toda a salmoura do cartão da célula de baixo.
Nas duas primeiras décadas do séc. XIX, após a invenção da pilha, houve evolução acelerada na área da eletroquímica.
A seguir temos a proposta de um experimento para fazer uma pilha com moedas e papel alumínio.
Mais abaixo, nas referências, há o endereço para uma tradução da carta original de Alessandro Volta à Royal Society, comunicando a invenção da pilha voltaica.
Experimento: Pilha Voltaica
Para realizar este experimento será necessário:- 10 moedas de R$ 0,05 (de cobre)
- 1 moeda de R$ 0,25 ou R$ 0,50 (ou um compasso)
- 1 folha de papel sulfite
- 1 pedaço de papel alumínio
- 1 pedaço de fita crepe
- 2 pedaços de fio elétrico flexível (fio fino)
- 1/2 copo de vinagre
- 1 colher de sal
- 1 LED vermelho (diodo emissor de luz)
- Misture a colher de sal em meio copo de vinagre e dissolva o máximo possível.
- Corte 9 círculos de papel alumínio do tamanho da moeda de R$ 0,05.
- Corte 9 círculos de papel sulfite de diâmetro pouco maior que o anterior, do tamanho da moeda de R$ 0,25 ou R$ 0,50.
- Vá empilhando as moedas e os círculos de papel sulfite e alumínio conforme mostrado na figura abaixo, na seguinte ordem: moeda, papel sulfite molhado no vinagre com sal, papel alumínio; e vá repetindo (a) (b). Mergulhe os círculos de papel sulfite no vinagre com sal e deixe por alguns segundos antes de colocar na pilha. (c) Finalize o empilhamento colocando uma moeda de 5 centavos sobre o último disco de papel alumínio, sem colocar o papel sulfite entre eles.

- (d) Conecte os dois terminais do LED utilizando fios, assim como mostrado na figura, às extremidades da pilha. O LED deve acender. Caso não acenda, a polaridade pode estar invertida. Tente invertendo os terminais. Esta pilha produz aproximadamente uma diferença de potencial de 2,5V.
Referências
MAGNAGHI, C. P.; ASSIS, A. K. T.; Sobre a eletricidade excitada pelo simples contato entre substâncias condutoras de tipos diferentes - Uma tradução comentada do artigo de volta de 1800 descrevendo sua invenção da pilha elétrica, Caderno Brasileiro de Ensino de Física, v. 25, n. 1: p. 118-140, abr. 2008. Disponível em <http://dx.doi.org/10.5007/2175-7941.2008v25n1p118>. Acessado em 02 mar. 2016.quarta-feira, 2 de março de 2016
Grandezas Físicas e o Sistema Internacional de Unidades (SI)
Uma grandeza física é um valor obtido através de medição. As grandezas físicas podem ser de dois tipos:
Grandezas Escalares
Possuem somente valor (magnitude) numéricoEx: Temperatura, volume, tempo, massa, densidade.
Grandezas Vetoriais
Possuem valor (magnitude, módulo), direção e sentido.Ex: Força, velocidade, aceleração, impulso.
As grandezas físicas são expressas através de unidades padronizadas. No Brasil adotamos o Sistema Internacional de unidades.
Sistema Internacional de Unidades (SI)
O Sistema Internacional de Unidades, geralmente referido pela sigla SI, é forma moderna do sistema métrico. Consiste num sistema de unidades de medida concebido em torno de sete unidades básicas e da conveniência do número dez (base decimal).
Unidades básicas
Grandezas de base
| Grandeza de Base | Símbolo | Unidade de Base | Símbolo | |
| comprimento | l, h, r, x | metro | m | |
| massa | m | quilograma | kg | |
| tempo, duração | t | segundo | s | |
| corrente elétrica | I,i | ampere | A | |
| temperatura termodinâmica | T | kelvin | K | |
| quantidade de substância | n | mol | mol | |
| intensidade luminosa | Iv | candela | cd |
Grandezas derivadas
Prefixos
| Fator | Nome | Símbolo | Fator | Nome | Símbolo | |
| 101 | deca | da | 10-1 | deci | d | |
| 102 | hecto | h | 10-2 | centi | c | |
| 103 | quilo | k | 10-3 | mili | m | |
| 106 | mega | M | 10-6 | micro | µ | |
| 109 | giga | G | 10-9 | nano | n | |
| 1012 | tera | T | 10-12 | pico | p | |
| 1015 | peta | P | 10-15 | femto | f | |
| 1018 | exa | E | 10-18 | atto | a | |
| 1021 | zetta | Z | 10-21 | zepto | z | |
| 1024 | yotta | Y | 10-24 | yocto | y |
Uma descrição do Sistema Internacional de Unidades pode ser encontrada na página do INMETRO - Instituto Nacional de Metrologia, Qualidade e Tecnologia, que regulamenta os padrões de metrologia no Brasil:
http://www.inmetro.gov.br/consumidor/pdf/Resumo_SI.pdf
A tradução completa do original em francês pode ser encontrada no endereço abaixo:
http://www.inmetro.gov.br/inovacao/publicacoes/si_versao_final.pdf
Notas de aula
quinta-feira, 25 de fevereiro de 2016
A Física como um programa de estudo unificado das Forças Fundamentais da Natureza
Desde os gregos antigos, como Aristóteles (séc. IV a.C.) e Arquimedes (séc. III a.C.), o conceito de força vem sendo elaborado.
Foi só com o trabalho coletivo da Royal Society (a Real Sociedade de Londres para o Melhoramento do Conhecimento Natural, que em inglês é chamada The Royal Society of London for the Improvement of Natural Knowledge) no séc. XVIII e especialmente o trabalho de Isaac Newton, foi que o conceito de força foi formalizado da maneira como conhecemos hoje:
"A força resultante que atua sobre um corpo é proporcional ao produto da massa pela aceleração por ele adquirida"
Ou, expressando na notação matemática:
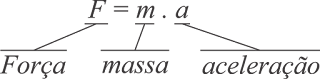
Desde então os fenômenos naturais vem sendo estudados pela física, em geral, através das forças que os produzem. Foram identificadas algumas forças fundamentais da natureza. São elas:
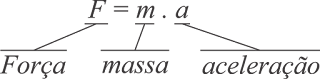
Esta equação define a força inercial e é chamada de 2ª Lei de Newton.
Desde então os fenômenos naturais vem sendo estudados pela física, em geral, através das forças que os produzem. Foram identificadas algumas forças fundamentais da natureza. São elas:
Posteriormente a teoria da eletricidade e do magnetismo foram unificadas por James Clerk Maxwell (séc. XIX) de maneira que hoje entende-se que elas são aspectos diferentes de um mesmo tipo de interação: a força eletromagnética.
A seguir serão mostrados fenômenos e descrições de onde poderemos observar as forças fundamentais da natureza.
Força gravitacional
A força gravitacional é uma força de interação entre corpos massivos, sempre atrativa. A força gravitacional é aquela que promove o movimento dos corpos em queda na superfície da Terra da mesma maneira que mantém a Lua em sua órbita através da atração.
Força elétrica
A força elétrica é aquela que se observa entre corpos carregados eletricamente. A força elétrica é atrativa entre cargas opostas (sinais diferentes) e é repulsiva entre cargas de mesmo sinal.Força Magnética
A força magnética é aquela que se observa entre imãs naturais (magnetita) e artificiais (outros compostos e também bobinas percorridas por uma corrente elétrica, chamados de eletroímãs). Assim como a força elétrica elas podem ser atrativas (quando os imãs estão orientados no mesmo sentido) ou repulsivas (quando os imãs estão orientados em sentido contrário).O imãs tem polos magnéticos identificados por Norte (N) e Sul (S). Ao contrário das cargas elétricas, os polos dos imãs não podem ser separados.
Forças Nucleares
As forças nucleares são as responsáveis por manter o núcleo do átomo estável. O núcleo é formado por prótons e nêutrons. Os prótons tem carga elétrica positiva (+). Em átomos com mais de um próton a força de repulsão elétrica entre os prótons é muito grande, pois eles estão muito próximos. Há uma força de curto alcance que mantém os prótons e nêutrons unidos no núcleo, chamada de Força Nuclear Forte.
Há também partículas menores que os prótons, nêutrons e elétrons, chamadas de neutrinos. Estas partículas surgem na decomposição do nêutron (decaimento radioativo) e são relacionadas com a força que expulsa elétrons de alta velocidade do átomo que se formam a partir do nêutron nesta decomposição radioativa. Esta é a chamada Força Nuclear Fraca.
Conclusão
Como foi dito anteriormente, as forças elétrica e magnética estão relacionadas, sendo dois aspectos diferentes de uma mesma força fundamental, chamada de Força Eletromagnética. Assim podemos dizer que existem 4 tipos de forças fundamentais:- Força Gravitacional
- Força Eletromagnética
- Força Nuclear Forte
- Força Nuclear Fraca
quinta-feira, 11 de fevereiro de 2016
Calculadora científica - Ferramenta para a Solução Literal de Problemas de Física, Química e Matemática
* Esta página está em permanente construção
A pesquisa em toda a área da Ciência e da Tecnologia, o estudo da Economia, os projetos das Engenharias, as previsões da Meteorologia, as Telecomunicações, as operações financeiras que movem as Bolsas e os Mercados, as pesquisas científicas, em resumo: tudo que move o mundo moderno - todas essas coisas são baseadas na Matemática. A vida do humano moderno é baseada na Matemática.
A Matemática modela o mundo Físico. É como se a Física fosse a Poesia e a Matemática a Linguagem.
Apesar de, no aprendizado da Matemática e da Física, realizar cálculos com papel e lápis serem fundamentais, não é assim que acontece na vida real, no mundo moderno. Toda a Matemática que roda as engrenagens do mundo moderno é executada através de computadores programados para realizar tais tarefas.
Nos trabalhos reais da Física, das Engenharias e das Ciências de uma forma geral o computador é utilizado para a solução de problemas, simulações de modelos, cálculos para projetos, etc. Neste sentido é importante conhecer como utilizar a matemática através das ferramentas de cálculo dos computadores.
A principal característica destas ferramentas computacionais que diferem elas de uma simples calculadora é que elas são capazes de lidar com matemática simbólica. Isto quer dizer que realizam cálculos não só com números, mas também com variáveis e funções.
Com esta ferramenta você poderá entender melhor como é o dia-a-dia de trabalho da maior parte dos físicos, matemáticos, engenheiros e pesquisadores de uma forma geral através da ferramenta de cálculos que está ao final desta página. Ela consiste basicamente de uma calculadora científica onde é possível especificar os passos para a solução de um problema e ela executará os cálculos numéricos para chegar à solução. Além disso esta calculadora científica possui definições de constantes matemáticas e físicas.
Esta ferramenta de cálculo funciona da seguinte forma: você digita na caixa de texto abaixo definindo valores, constantes, expressões matemáticas e funções, da mesma maneira que faz ao interpretar um problema de física e anotar os valores dados no exercício, as equações e fórmulas que serão utilizadas para fazer o cálculo, então clica no botão resolver. Se você digitar todos os comandos matemáticos de forma correta, as funções necessárias para o cálculo corretas, definir todos os valores necessários para calcular,
o programa fará todo o cálculo, mostrando os valores numéricos passo-a-passo.
Mas, ATENÇÃO! O programa simplesmente irá calcular o que você programar. O programa NÃO IRÁ PENSAR POR VOCÊ. Você precisará INTERPRETAR O ENUNCIADO DO PROBLEMA, precisará conhecer como são dados comandos ao programa para DEFINIR VALORES INICIAIS e ESCREVER ADEQUADAMENTE AS EQUAÇÕES E FUNÇÕES MATEMÁTICAS, tomando o cuidado de CONVERTER AS UNIDADES, pois elas não são calculadas pelo programa.
Instruções de operação:
Lista de funções matemáticas
Lista de funções para Matrizes
Lista de constantes físicas
Fonte: http://physics.nist.gov/cuu/Constants/
Lista de número atômico e massa molar dos elementos químicos
A pesquisa em toda a área da Ciência e da Tecnologia, o estudo da Economia, os projetos das Engenharias, as previsões da Meteorologia, as Telecomunicações, as operações financeiras que movem as Bolsas e os Mercados, as pesquisas científicas, em resumo: tudo que move o mundo moderno - todas essas coisas são baseadas na Matemática. A vida do humano moderno é baseada na Matemática.
A Matemática modela o mundo Físico. É como se a Física fosse a Poesia e a Matemática a Linguagem.
Apesar de, no aprendizado da Matemática e da Física, realizar cálculos com papel e lápis serem fundamentais, não é assim que acontece na vida real, no mundo moderno. Toda a Matemática que roda as engrenagens do mundo moderno é executada através de computadores programados para realizar tais tarefas.
Nos trabalhos reais da Física, das Engenharias e das Ciências de uma forma geral o computador é utilizado para a solução de problemas, simulações de modelos, cálculos para projetos, etc. Neste sentido é importante conhecer como utilizar a matemática através das ferramentas de cálculo dos computadores.
A principal característica destas ferramentas computacionais que diferem elas de uma simples calculadora é que elas são capazes de lidar com matemática simbólica. Isto quer dizer que realizam cálculos não só com números, mas também com variáveis e funções.
Com esta ferramenta você poderá entender melhor como é o dia-a-dia de trabalho da maior parte dos físicos, matemáticos, engenheiros e pesquisadores de uma forma geral através da ferramenta de cálculos que está ao final desta página. Ela consiste basicamente de uma calculadora científica onde é possível especificar os passos para a solução de um problema e ela executará os cálculos numéricos para chegar à solução. Além disso esta calculadora científica possui definições de constantes matemáticas e físicas.
Esta ferramenta de cálculo funciona da seguinte forma: você digita na caixa de texto abaixo definindo valores, constantes, expressões matemáticas e funções, da mesma maneira que faz ao interpretar um problema de física e anotar os valores dados no exercício, as equações e fórmulas que serão utilizadas para fazer o cálculo, então clica no botão resolver. Se você digitar todos os comandos matemáticos de forma correta, as funções necessárias para o cálculo corretas, definir todos os valores necessários para calcular,
o programa fará todo o cálculo, mostrando os valores numéricos passo-a-passo.
Mas, ATENÇÃO! O programa simplesmente irá calcular o que você programar. O programa NÃO IRÁ PENSAR POR VOCÊ. Você precisará INTERPRETAR O ENUNCIADO DO PROBLEMA, precisará conhecer como são dados comandos ao programa para DEFINIR VALORES INICIAIS e ESCREVER ADEQUADAMENTE AS EQUAÇÕES E FUNÇÕES MATEMÁTICAS, tomando o cuidado de CONVERTER AS UNIDADES, pois elas não são calculadas pelo programa.
Instruções de operação:
- As seguintes operações estão definidas sobre números reais e matrizes:
- soma +
- subtração -
- multiplicação *
- divisão /
- potência ^ ou **
- A operação fatorial (!) é definida sobre os números reais.
Exemplo:
6! = 6 • 5 • 4 • 3 • 2 • 1 - O dígito decimal é o ponto (.) e os valores numéricos podem ser expressos através de potências de 10, na notação científica, através da letra 'e':
Exemplos:
- 6.67408e-11 representa 6.67408 • 10-11
- 1e3 representa 1 • 103 = 1000
- Cada linha de comando pode ser de um dos 5 tipos: definição de número ou matriz, definição de função, expressão a computar, anotação ou linha em branco.
- definição de número ou matriz
Exemplos: - x = 10 (um número real)
- x = 10 * 3 (um valor numérico a calcular)
- v = S/t (uma expressão com valores definidos anteriormente)
- y = f(x) (uma expressão com funções definidas anteriormente)
- A = [[1,2,0],[1,1,0],[-1,4,0]] (uma matriz)
- definição de função
Exemplos: - # definição da função horária do movimento uniforme
s ( v, t ) = s0 + v * t - # definição da função energia cinética
Ec ( m, v ) = m * v^2 / 2 - expressão a computar
Exemplos:- 2 + 3 * 4
- As anotações são linhas iniciadas com o caractere #.
- As linhas em branco são ignoradas.
- Há funções e constantes (matemáticas e físicas) predefinidas:
Exemplos:- raiz ( radicando ) ou
raiz ( índice, radicando ) - log ( base,logaritmando )
- cte.pi
- cte.mi0
- raiz ( radicando ) ou
| constante | símbolo | uso na calculadora | Valor |
|---|---|---|---|
| pi | π | cte.pi | 3.141592653589793... |
| e | e | cte.e | 2.718281828459045... |
| função | uso na calculadora | Descrição | |||||||
|---|---|---|---|---|---|---|---|---|---|
| raiz | raiz(radicando) ou raiz(indice, radicando) | Calcula a raiz. Se for especificado somente um argumento calcula a raiz quadrada. Se forem especificados dois argumentos o primeiro é o índice, o segundo o radicando. | |||||||
| logaritmo | log(logaritmando) ou log(base, logaritmando) | Calcula o logaritmo. Se for especificado somente um argumento calcula o logarítmo na base 10. | |||||||
| logaritmo natural (neperiano) | ln(logaritmando) | Calcula o logarítmo de base natural (neperiano). | |||||||
| exponencial | exp(x) ou exponencial(x) | Calcula a exponencial de x ( ex ) | |||||||
| módulo (valor absoluto) | abs(x) ou absoluto(x) ou mod(x) ou modulo(x)ou |x| | Calcula o módulo, isto é, o valor absoluto de x ( |x| ) | |||||||
| seno | sen(x) | Calcula o seno de x | |||||||
| cosseno | cos(x) | Calcula o cosseno de x | |||||||
| tangente | tg(x) | Calcula a tangente de x | |||||||
| arco seno | asen(x) | Calcula o arco seno de x ( sen-1(x) ) | |||||||
| arco coseno | acos(x) | Calcula o arco cosseno de x ( cos-1(x) ) | |||||||
| arco tangente | atg(x) | Calcula o arco tangente de x ( tg-1(x) ) | |||||||
| seno hiperbólico | senh(x) | Calcula o seno hiperbólico de x | |||||||
| cosseno hiperbólico | cosh(x) | Calcula o cosseno hiperbólico de x | |||||||
| tangente hiperbólica | tgh(x) | Calcula a tangente hiperbólica de x | |||||||
| arco seno hiperbólico | asenh(x) | Calcula o arco seno hiperbólico de x ( senh-1(x) ) | |||||||
| arco coseno hiperbólico | acosh(x) | Calcula o arco cosseno hiperbólico de x ( cosh-1(x) ) | |||||||
| arco tangente hiperbólica | atgh(x) | Calcula o arco tangente hiperbólico de x ( tgh-1(x) ) | |||||||
| binomial | binomial(n,k) | Calcula o binomial
|
Lista de funções para Matrizes
| função | uso na calculadora | Descrição |
|---|---|---|
| matriz | matriz(linhas, colunas, <valor padrão>) | Cria matriz preenchendo com o valor padrão (opcional, 0 se não fornecido). |
| número de linhas | linhas(matriz) | Obtém o número de linhas da matriz. |
| número de colunas | colunas(matriz) | Obtém o número de colunas da matriz. |
| identidade | ident(dimensão) | Retorna matriz identidade de uma dada ordem. |
| transposta | trans(matriz) | Calcula a matriz transposta. |
| determinante | det(matriz) | Calcula o determinante da matriz. |
| traço | traco(matriz) | Calcula o traço da matriz. |
| inversa | inv(matriz) | Calcula a matriz inversa. |
| aplicação do Método de Gauss | gauss(matriz, vetor) | Aplicação do método de Gauss para a solução de sistemas lineares. |
Lista de constantes físicas
| constante | símbolo | uso na calculadora | Valor | Unidade |
|---|---|---|---|---|
| Aceleração da gravidade | g | cte.g | 9.80665 | m s-2 |
| Constante gravitacional | G | cte.G | 6.67408e-11 | m3 kg-1 s-2 |
| Número de Avogadro | N0 | cte.N0 | 6.022140857e23 | mol-1 |
| Atmosfera padrão | atm | cte.atm | 1.01325e5 | Pa |
| Constante dos gases ideais | R | cte.R | 8.3144598 | J mol-1 K-1 |
| Constante de Boltzmann | k | cte.k | 1.38064852e-23 | J K-1 |
| Carga elementar | e | cte.ee | 1.6021766208e-19 | C |
| Massa do elétron | me | cte.me | 9.10938356e-31 | kg |
| Permissividade elétrica do vácuo | ϵ0 | cte.ep0 | 8.854187817e-12 | F m-1 |
| Permeabilidade magnética do vácuo | μ0 | cte.mi0 | 4*cte.pi*1e-7 | N A-2 |
| Velocidade da luz no vácuo | c0 | cte.c0 | 2.99792458e8 | m s-1 |
| Constante de Planck | h | cte.h | 6.626070040e-34 | J s mol-1 |
Lista de número atômico e massa molar dos elementos químicos
| Símbolo | Elemento | Número atômico | Massa molar | ||
|---|---|---|---|---|---|
| Valor | Uso na calculadora | Valor (g/mol) | Uso na calculadora | ||
| H | Hidrogênio | 1 | cte.Z_H | 1.007947 | cte.M_H |
| He | Hélio | 2 | cte.Z_He | 4.0026022 | cte.M_He |
| Li | Lítio | 3 | cte.Z_Li | 6.9412 | cte.M_Li |
| Be | Berílio | 4 | cte.Z_Be | 9.0121823 | cte.M_Be |
| B | Boro | 5 | cte.Z_B | 10.8117 | cte.M_B |
| C | Carbono | 6 | cte.Z_C | 12.01078 | cte.M_C |
| N | Nitrogênio | 7 | cte.Z_N | 14.00672 | cte.M_N |
| O | Oxigênio | 8 | cte.Z_O | 15.99943 | cte.M_O |
| F | Flúor | 9 | cte.Z_F | 18.99840325 | cte.M_F |
| Ne | Neônio | 10 | cte.Z_Ne | 20.17976 | cte.M_Ne |
| Na | Sódio | 11 | cte.Z_Na | 22.98976928 | cte.M_Na |
| Mg | Magnésio | 12 | cte.Z_Mg | 24.30506 | cte.M_Mg |
| Al | Alumínio | 13 | cte.Z_Al | 26.98153868 | cte.M_Al |
| Si | Silício | 14 | cte.Z_Si | 28.08553 | cte.M_Si |
| P | Fósforo | 15 | cte.Z_P | 30.9737622 | cte.M_P |
| S | Enxofre | 16 | cte.Z_S | 32.0655 | cte.M_S |
| Cl | Cloro | 17 | cte.Z_Cl | 35.4532 | cte.M_Cl |
| Ar | Argônio | 18 | cte.Z_Ar | 39.9481 | cte.M_Ar |
| K | Potássio | 19 | cte.Z_K | 39.09831 | cte.M_K |
| Ca | Cálcio | 20 | cte.Z_Ca | 40.0784 | cte.M_Ca |
| Sc | Escândio | 21 | cte.Z_Sc | 44.9559126 | cte.M_Sc |
| Ti | Titânio | 22 | cte.Z_Ti | 47.8671 | cte.M_Ti |
| V | Vanádio | 23 | cte.Z_V | 50.94151 | cte.M_V |
| Cr | Cromo | 24 | cte.Z_Cr | 51.99616 | cte.M_Cr |
| Mn | Manganês | 25 | cte.Z_Mn | 54.9380455 | cte.M_Mn |
| Fe | Ferro | 26 | cte.Z_Fe | 55.8452 | cte.M_Fe |
| Co | Cobalto | 27 | cte.Z_Co | 58.9331955 | cte.M_Co |
| Ni | Níquel | 28 | cte.Z_Ni | 58.69342 | cte.M_Ni |
| Cu | Cobre | 29 | cte.Z_Cu | 63.5463 | cte.M_Cu |
| Zn | Zinco | 30 | cte.Z_Zn | 65.4094 | cte.M_Zn |
| Ga | Gálio | 31 | cte.Z_Ga | 69.7231 | cte.M_Ga |
| Ge | Germânio | 32 | cte.Z_Ge | 72.641 | cte.M_Ge |
| As | Arsênio | 33 | cte.Z_As | 74.921602 | cte.M_As |
| Se | Selênio | 34 | cte.Z_Se | 78.963 | cte.M_Se |
| Br | Bromo | 35 | cte.Z_Br | 79.9041 | cte.M_Br |
| Kr | Criptônio | 36 | cte.Z_Kr | 83.7982 | cte.M_Kr |
| Rb | Rubídio | 37 | cte.Z_Rb | 85.46783 | cte.M_Rb |
| Sr | Estrôncio | 38 | cte.Z_Sr | 87.621 | cte.M_Sr |
| Y | Ítrio | 39 | cte.Z_Y | 88.905852 | cte.M_Y |
| Zr | Zircônio | 40 | cte.Z_Zr | 91.2242 | cte.M_Zr |
| Nb | Nióbio | 41 | cte.Z_Nb | 92.906382 | cte.M_Nb |
| Mo | Molibdênio | 42 | cte.Z_Mo | 95.942 | cte.M_Mo |
| Tc | Tecnécio | 43 | cte.Z_Tc | 98 | cte.M_Tc |
| Ru | Rutênio | 44 | cte.Z_Ru | 101.072 | cte.M_Ru |
| Rh | Ródio | 45 | cte.Z_Rh | 102.905502 | cte.M_Rh |
| Pd | Paládio | 46 | cte.Z_Pd | 106.421 | cte.M_Pd |
| Ag | Prata | 47 | cte.Z_Ag | 107.86822 | cte.M_Ag |
| Cd | Cádmio | 48 | cte.Z_Cd | 112.4118 | cte.M_Cd |
| In | Índio | 49 | cte.Z_In | 114.8183 | cte.M_In |
| Sn | Estanho | 50 | cte.Z_Sn | 118.7107 | cte.M_Sn |
| Sb | Antimónio | 51 | cte.Z_Sb | 121.7601 | cte.M_Sb |
| Te | Telúrio | 52 | cte.Z_Te | 128.603 | cte.M_Te |
| I | Iodo | 53 | cte.Z_I | 126.904473 | cte.M_I |
| Xe | Xenônio | 54 | cte.Z_Xe | 131.2936 | cte.M_Xe |
| Cs | Césio | 55 | cte.Z_Cs | 132.9054519 | cte.M_Cs |
| Ba | Bário | 56 | cte.Z_Ba | 137.3277 | cte.M_Ba |
| La | Lantânio | 57 | cte.Z_La | 138.905477 | cte.M_La |
| Ce | Cério | 58 | cte.Z_Ce | 140.1161 | cte.M_Ce |
| Pr | Praseodímio | 59 | cte.Z_Pr | 140.907652 | cte.M_Pr |
| Nd | Neodímio | 60 | cte.Z_Nd | 144.2423 | cte.M_Nd |
| Pm | Promécio | 61 | cte.Z_Pm | 145 | cte.M_Pm |
| Sm | Samário | 62 | cte.Z_Sm | 150.362 | cte.M_Sm |
| Eu | Európio | 63 | cte.Z_Eu | 151.9641 | cte.M_Eu |
| Gd | Gadolínio | 64 | cte.Z_Gd | 157.253 | cte.M_Gd |
| Tb | Térbio | 65 | cte.Z_Tb | 158.925352 | cte.M_Tb |
| Dy | Disprósio | 66 | cte.Z_Dy | 162.5001 | cte.M_Dy |
| Ho | Hólmio | 67 | cte.Z_Ho | 164.930322 | cte.M_Ho |
| Er | Érbio | 68 | cte.Z_Er | 167.2593 | cte.M_Er |
| Tm | Túlio | 69 | cte.Z_Tm | 168.934212 | cte.M_Tm |
| Yb | Itérbio | 70 | cte.Z_Yb | 173.043 | cte.M_Yb |
| Lu | Lutécio | 71 | cte.Z_Lu | 174.9671 | cte.M_Lu |
| Hf | Háfnio | 72 | cte.Z_Hf | 178.492 | cte.M_Hf |
| Ta | Tântalo | 73 | cte.Z_Ta | 180.947882 | cte.M_Ta |
| W | Tungsténio | 74 | cte.Z_W | 183.841 | cte.M_W |
| Re | Rênio | 75 | cte.Z_Re | 186.2071 | cte.M_Re |
| Os | Ósmio | 76 | cte.Z_Os | 190.233 | cte.M_Os |
| Ir | Irídio | 77 | cte.Z_Ir | 192.2173 | cte.M_Ir |
| Pt | Platina | 78 | cte.Z_Pt | 195.0849 | cte.M_Pt |
| Au | Ouro | 79 | cte.Z_Au | 196.9665694 | cte.M_Au |
| Hg | Mercúrio | 80 | cte.Z_Hg | 200.592 | cte.M_Hg |
| Tl | Tálio | 81 | cte.Z_Tl | 204.38332 | cte.M_Tl |
| Pb | Chumbo | 82 | cte.Z_Pb | 207.21 | cte.M_Pb |
| Bi | Bismuto | 83 | cte.Z_Bi | 208.980401 | cte.M_Bi |
| Po | Polônio | 84 | cte.Z_Po | 210 | cte.M_Po |
| At | Astato | 85 | cte.Z_At | 210 | cte.M_At |
| Rn | Radônio | 86 | cte.Z_Rn | 220 | cte.M_Rn |
| Fr | Frâncio | 87 | cte.Z_Fr | 223 | cte.M_Fr |
| Ra | Rádio | 88 | cte.Z_Ra | 226 | cte.M_Ra |
| Ac | Actínio | 89 | cte.Z_Ac | 227 | cte.M_Ac |
| Th | Tório | 90 | cte.Z_Th | 232.038062 | cte.M_Th |
| Pa | Protactínio | 91 | cte.Z_Pa | 231.035882 | cte.M_Pa |
| U | Urânio | 92 | cte.Z_U | 238.028913 | cte.M_U |
| Np | Netúnio | 93 | cte.Z_Np | 237 | cte.M_Np |
| Pu | Plutônio | 94 | cte.Z_Pu | 244 | cte.M_Pu |
| Am | Amerício | 95 | cte.Z_Am | 243 | cte.M_Am |
| Cm | Cúrio | 96 | cte.Z_Cm | 247 | cte.M_Cm |
| Bk | Berquélio | 97 | cte.Z_Bk | 247 | cte.M_Bk |
| Cf | Califórnio | 98 | cte.Z_Cf | 251 | cte.M_Cf |
| Es | Einstênio | 99 | cte.Z_Es | 252 | cte.M_Es |
| Fm | Férmio | 100 | cte.Z_Fm | 257 | cte.M_Fm |
| Md | Mendelévio | 101 | cte.Z_Md | 258 | cte.M_Md |
| No | Nobélio | 102 | cte.Z_No | 259 | cte.M_No |
| Lr | Laurêncio | 103 | cte.Z_Lr | 262 | cte.M_Lr |
| Rf | Rutherfórdio | 104 | cte.Z_Rf | 261 | cte.M_Rf |
| Db | Dúbnio | 105 | cte.Z_Db | 262 | cte.M_Db |
| Sg | Seabórgio | 106 | cte.Z_Sg | 266 | cte.M_Sg |
| Bh | Bório | 107 | cte.Z_Bh | 264 | cte.M_Bh |
| Hs | Hássio | 108 | cte.Z_Hs | 277 | cte.M_Hs |
| Mt | Meitnério | 109 | cte.Z_Mt | 268 | cte.M_Mt |
| Ds | Darmstácio | 110 | cte.Z_Ds | 271 | cte.M_Ds |
| Rg | Roentgênio | 111 | cte.Z_Rg | 272 | cte.M_Rg |
| Cn | Copernício | 112 | cte.Z_Cn | 277 | cte.M_Cn |
| Uut | Unúntrio | 113 | cte.Z_Uut | 284 | cte.M_Uut |
| Fl | Fleróvio | 114 | cte.Z_Fl | 289 | cte.M_Fl |
| Uup | Ununpêntio | 115 | cte.Z_Uup | 288 | cte.M_Uup |
| Lv | Livermório | 116 | cte.Z_Lv | 292 | cte.M_Lv |
| Uus | Ununséptio | 117 | cte.Z_Uus | 288 | cte.M_Uus |
| Uuo | Ununóctio | 118 | cte.Z_Uuo | 294 | cte.M_Uuo |
Gráficos
A função predefinida grafico permite desenhar gráficos como mostrado na sintaxe a seguir:
grafico ( expressão, variável eixo x, mínimo eixo x, máximo eixo x )Por exemplo, a função abaixo mostra o gráfico da parábola:
grafico ( x^2, x, -4, 4 )
Problemas exemplo
Abaixo seguem exemplos de resolução de cálculos de problemas de Física. Interprete os problemas e observe como são definidos os valores e convertidos em unidades do SI. Clique no botão colar resolução para a resolução do problema ser colada na caixa de texto de solução da calculadora científica e clique no botão Resolver. O cálculo passo-a-passo aparecerá abaixo da caixa de texto da solução.Solução da equação e gráfico da função de segundo grau.
x2 - 10 x + 24 = 0
Resolução:
# Solução da equação de 2º grau: x^2-10*x+24=0 # definição dos coeficientes a = 1 b = -10 c = 21 # solução pela fórmula de Bhaskara delta = b^2-4*a*c x1 = (-b + raiz(delta))/(2*a) x2 = (-b - raiz(delta))/(2*a) # definição da função de 2º grau f(x) = a*x^2+b*x+c # mostra gráfico de f(x) no intervalo x=[-1,8] grafico (f(x),x,-1,8)
Operações com matrizes.
Resolução:
# Cria a matriz 3x3 com elementos nulos A = matriz(3,3) A # Cria a matriz 3x3 com elementos selecionados (20) A = matriz(3,3,20) A # Cria a matriz identidade 3x3 A = ident(3) A # Traço da matriz traco(A) # Define matrizes para operar A = [[1,2,0],[1,1,0],[-1,4,0]] B = [[1,2,3],[1,1,-1],[2,2,2]] C = [[1,2,3],[1,1,-1],[1,1,1]] D = [[2,1,-3],[3,2,4],[2,5,-2]] E = [[1,3,-9,5],[2,-3,-5,5],[2,8,-1,7],[3,-4,3,6]] # Soma F = A+B # Produto G = 2*A H = A*B I = A*C # Apesar de B diferente de C o produto A*B e A*C resulta igual # Divisão J = A/B # Matriz transposta K = trans(I) K # Determinante det(D) det(E) # Matriz inversa inv(E) # Potência E^-1 E^3 E^0 # Muda um elemento K[1,3] = 1e6 # Obtém um elemento K[1,1]
Calcule a distância de 1 ano-luz em quilômetros, sabendo que a velocidade da luz é c = 300000000 m/s.
Resolução:
# velocidade da luz em m/s c = 300000000 #Equação para calcular a distância em função da velocidade s(v,t) = v*t # Valor de 1 km em metros km = 1000 #Valor de 1 ano em segundos ano = 365*24*60*60 ano_luz = s(c,ano)/km
Calcule a potência média em watts, dissipada por uma pessoa na forma de trabalho ou calor, através do consumo calórico diário médio para o homem e para a mulher, onde o consumo diário masculino é dado por Cdm = 3500 kcal/dia e o feminino por Cdf = 3000 kcal/dia. Observação: 1 caloria equivale exatamente a 4,1868 Joules.
Resolução:
# Valor da caloria em Joules cal = 4.1868 #Valor do dia em segundos dia = 24*60*60 #Valor da Quilocaloria em Joules kcal = 1e3*cal #Resultado: Cdm = 3500*kcal/dia Cdf = 3000*kcal/dia
De quantas maneiras diferentes podemos dispor, numa mesma prateleira de uma estante, quatro livros de matemática e três livros de física, de modo que livros de mesma matéria permaneçam juntos?
A) 280 modos diferentes
B) 288 modos diferentes
C) 144 modos diferentes
D) 196 modos diferentes
E) 344 modos diferentes
Resolução:
4!*3!*2
ENEM 2015 - A radiação ultravioleta (UV) é dividida, de acordo com três faixas de frequência, em UV-A, UV-B e UV-C, conforme a figura.
Para selecionar um filtro solar que apresente absorção máxima na faixa UV-B, uma pessoa analisou os espectros de absorção da radiação UV de cinco filtros solares:
Considere:
velocidade da luz = 3,0×108 m/s e 1 nm = 1,0×10-9 m.
O filtro solar que a pessoa deve selecionar é o
A) V.
B) IV.
C) III.
D) II.
E) I.
Resolução:
# Dados do exercício: # Velocidade da luz e nanometro c = 3e8 nm = 1e-9 # Limite inferior e superior da frequência da faixa UV-B f_uvb_inferior = 9.34e14 f_uvb_superior = 1.03e15 lambda(f) = (c/f) / nm # Comprimento de onda dos limites da faixa UV-B lambda_uvb_superior = lambda(f_uvb_inferior) lambda_uvb_inferior = lambda(f_uvb_superior)
ENEM 2015 - Um carro solar é um veículo que utiliza apenas a energia solar para a sua locomoção. Tipicamente, o carro contém um painel fotovoltaico que converte a energia do Sol em energia elétrica que, por sua vez, alimenta um motor elétrico. A imagem mostra o carro solar Tokai Challenger, desenvolvido na Universidade de Tokai, no Japão, e que venceu o World Solar Challenge de 2009, uma corrida internacional de carros solares, tendo atingido uma velocidade média acima de 100 km/h.
Considere uma região plana onde a insolação (energia solar por unidade de tempo e de área que chega à superfície da Terra) seja de 1 000 W/m2, que o carro solar possua massa de 200 kg e seja construído de forma que o painel fotovoltaico em seu topo tenha uma área de 9,0 m2 e rendimento de 30%.
Desprezando as forças de resistência do ar, o tempo que esse carro solar levaria, a partir do repouso, para atingir a velocidade de 108 km/h é um valor mais próximo de
A) 1,0 s.
B) 4,0 s.
C) 10 s.
D) 33 s.
E) 300 s.
Resolução:
# Dados do exercício: # Densidade superficial de potência da energia solar: D = 1000 # Massa do carro m = 200 # Área do painel A = 9 # Rendimento r = 30/100 # Velocidade v = 108 #Fatores de conversão para o SI: # valor da hora em segundos hora = 60*60 # valor do quilômetro em metros km = 1000 # Velocidade no SI: v = v * km / hora # Potência efetiva P = D*A*r # Energia Cinética E = m*v^2/2 # Tempo para atingir a velocidade média t = E / P
ENEM 2015 - A hidroponia pode ser definida como uma técnica de produção de vegetais sem necessariamente a presença de solo. Uma das formas de implementação é manter as plantas com suas raízes suspensas em meio líquido, de onde retiram os nutrientes essenciais.
Suponha que um produtor de rúcula hidropônica precise ajustar a concentração do íon nitrato (NO3-) para 0,009 mol/L em um tanque de 5 000 litros e, para tanto, tem em mãos uma solução comercial nutritiva de nitrato de cálcio 90 g/L. As massas molares dos elementos N, O e Ca são iguais a 14 g/mol, 16 g/mol e 40 g/mol, respectivamente.
Qual o valor mais próximo do volume da solução nutritiva, em litros, que o produtor deve adicionar ao tanque?
A) 26
B) 41
C) 45
D) 51
E) 82
Resolução:
# Dados do exercício: # Dados do exercício: # nitrato de cálcio Ca(NO3)2 # massas molares: m_mol_N = 14 m_mol_O = 16 m_mol_Ca = 40 m_mol_NO3 = m_mol_N + m_mol_O * 3 m_mol_Ca_NO3_2 = m_mol_Ca + m_mol_NO3 * 2 concentr_NO3 = 0.009 concentr_solucao = 90 V_tanque = 5e3 V = (concentr_NO3/2) / (concentr_solucao/m_mol_Ca_NO3_2) * V_tanque
ENEM 2015 - Uma análise criteriosa do desempenho de Usain Bolt na quebra do recorde mundial dos 100 metros rasos mostrou que, apesar de ser o último dos corredores a reagir ao tiro e iniciar a corrida, seus primeiros 30 metros foram os mais velozes já feitos em um recorde mundial, cruzando essa marca em 3,78 segundos. Até se colocar com o corpo reto, foram 13 passadas, mostrando sua potência durante a aceleração, o momento mais importante da corrida. Ao final deste percurso, Bolt havia atingido a velocidade máxima de 12 m/s.
Supondo que a massa desse corredor seja igual a 90 kg, o trabalho total realizado nas 13 primeiras passadas é mais próximo de:
A) 5,4×102 J.
B) 6,5×103 J.
C) 8,6×103 J.
D) 1,3×104 J.
E) 3,2×104 J.
Resolução:
# Dados do exercício: # Massa do corredor m = 90 # Velocidade v = 12 # Trabalho realizado = Energia Cinética E = m*v^2/2
ENEM 2015 - Uma garrafa térmica tem como função evitar a troca de calor entre o líquido nela contido e o ambiente, mantendo a temperatura de seu conteúdo constante. Uma forma de orientar os consumidores na compra de uma garrafa térmica seria criar um selo de qualidade, como se faz atualmente para informar o consumo de energia de eletrodomésticos. o selo identificaria cinco categorias e informaria a variação de temperatura do conteúdo da garrafa, depois de decorridas seis horas de seu fechamento, por meio de uma porcentagem do valor inicial da temperatura de equilíbrio do líquido na garrafa. O quadro apresenta as categorias e os intervalos de variação percentual da temperatura.
| Tipo de selo | Variação de temperatura |
|---|---|
| A | menor que 10% |
| B | entre 10% e 25% |
| C | entre 25% e 40% |
| D | entre 40% e 55% |
| E | maior que 55% |
Para atribuir uma categoria a um modelo de garrafa térmica, são preparadas e misturadas, em uma garrafa, duas amostras de água, uma a 10ºC e outra a 40ºC, na proporção de um terço de água fria para dois terços de água quente. A garrafa é fechada. Seis horas depois, abre-se a garrafa e mede-se a temperatura da água, obtendo-se 16ºC.
Qual selo deveria ser posto na garrafa térmica testada?
A) A
B) B
C) C
D) D
E) E
Resolução:
# Dados do exercício: T_inicial = 2/3 * 40 + 1/3 * 10 T_final = 16 Variacao_percentual_T = T_final/T_inicial * 100
|
ATENÇÃO! Esta ferramenta de cálculo encontra-se em fase de construção e testes. Sempre verifique seus cálculos através de outros métodos. |
Assinar:
Comentários (Atom)







